サイコロ、ゾロ目 の確率 について サイコロを2つ振って12がそれぞれ1回ずつでる確率〜などの問題を考える時に、(12)(21)と2回分考えるのに ゾロ目のときは1回分しかカウントしない理由が直感的に分からずモヤモヤします。 モヤモヤを解決するヒントなど5 西尾眞喜子, 樋口保成 確率過程入門(確率論教程シリーズ3) 培風館06 年 6 飛田武幸 ブラウン運動岩波書店1975 年 7 I Karatzas, S E Shreve Brownian motion and stochastic calculus 1 区別のつかない2つのサイコロを投げ、その差が3以下になる確率 2 大小2つのサイコロを投げ、その差が3以下になる確率 3 同じサイコロを2回投げ、その差が3以下になる確率
確率は賭け事の理論
確率 サイコロ 3つ 同時
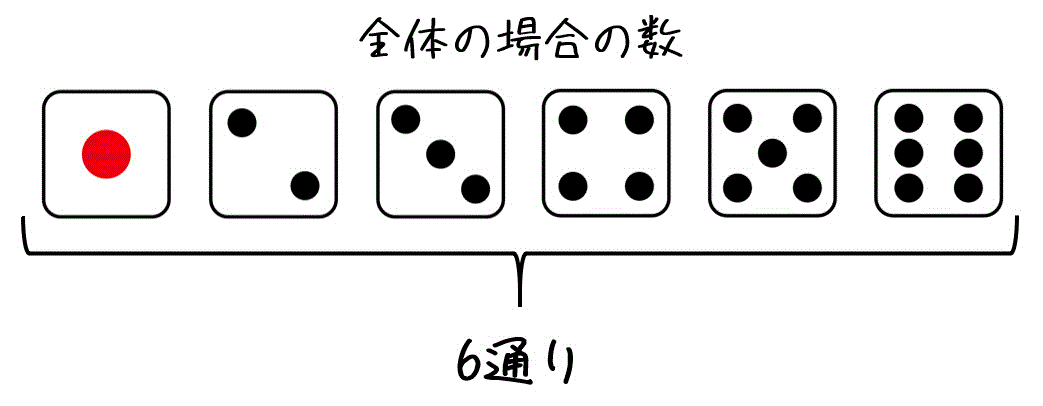
確率 サイコロ 3つ 同時- サイコロを1つ投げるとき、目の出方は 1,2,3,4,5,6 このように全部で6通りありますね。 この中から3の目は 1,2, 3,4,5,6 1通りしかありませんね。 だから、サイコロ1つを投げたとき、3の目が出る確率は $$\frac{1}{6}$$ となります。3 離散型確率変数 確率変数の種類 (離散型確率変数) サイコロの目や、晴れの時には「1」、曇りの時には「2」 のように離散的に値をとる確率変数を離散型確率変数 という。 (連続型確率変数) 株価収益率、身長、体重などのように連続的に値をとる



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト
〔例題例題例題 51 51 51〕 3 個のサイコロを投げて出る目の最大値と最小値の確率分布を求めよ. (解)3 個のサイコロの出る目を,それぞれ X,Y,Z ,目の最大値を表す確率変数 を Xmax とする.このとき,次のことが成り立つ.3 サイコロの確率 1.サイコロの確率 問題1 つぎの確率を考察せよ。 (1)1個のサイコロを2回投げて、2回とも1の目がでる確率。 (2)1個のサイコロを2回投げて、2回目に初めて1の目がでる確率。 最大値が1となるのは、 n 回とも1が出るときだけなので、確率は 1 6n 1 6 n となります。 これをふまえて、次の問題を考えてみましょう。 例題2 さいころを n 回ふる( n は2以上の整数)。 このとき、出た目の最大値が2になる確率を求めなさい。 最大値が2
問 区別のない 3 個のサイコロを投げるとき,出た目の和が 5 となる確率を求めよ.重複組合せ!?,と見せかけて,,,確率ほど基本の理解が このサイコロは、どの目も同じ確率で出る唯一のサイコロとして、高等学校の数学の教科書でも取り上げられました。 図1 入曽精密が造った完全重心のサイコロ(04年5月発表) 左が設計用の3dモデル。重心点を頂点とする6個の四角錐体の質量が完全に同じになるようにした。3dcadの特性と精緻 サイコロを5回投げて3の倍数が3回出る確率を教えてください。解き方がわかりません 0 回答 ぴじょん 1年以上前 中学生がどこまで知っているかわかりませんがなるべくわかりやすました🙏 0 ぴじょん 1年以上前 わかりやすました→わかりやすくしました (訂正) 0 この回答にコメント
例えば、サイコロを投げて出る目は{1, 2, 3, 4, 5, 6}のどれかです。 それぞれの目が出る確率は1/6ですから、 サイコロを投げて出る目は確率変数である と言えます。 この場合、確率変数の値(=サイコロの出る目)を「X」とすると、次のように表すことができます。 P (X)=1/6(X=1,2,3,4,5,6) 右側のカッコの中は「X」がとる値の範囲です。 簡単に言うと、 全部About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators確率変数(random variable) ある確率分布にしたがって定まる値 事象に付随する値という言い方もできる よく使う記号 X, Y, 例 くじ引き 事象 1等が当たる, 2等が当たる, はずれ 確率変数 賞金(1等 → 5000円, 2等 → 1000円, 3等 → 0円)




3個のさいころの出る目の最小値 Youtube



中学数学 確率
(1) 点 p が頂点Cに移動する確率を求めよ。 (2) この3枚のカードのときは,点 p が頂点Aに移動する確率は0である。そこで3枚のカードのうち, 6 だけを他の自然数が書かれたカードに交換して,点 p が頂点Aに移動する確率が0でないようにしたい。どのような自然数が書かれたカードに交換すればよいか,その自然数について,言葉や数,式などを使ってすべての場合を3つのサイコロを同時にふるとき,出る目の最大値と最小値を考える. (ⅰ) 最大値が3かつ最小値が2となる確率を求めよ. (ⅱ) 最大値と最小値の差が2以上となる確率を求めよ.例題6 1個のさいころを5回投げるとき,次の確率を求めよ。 (1) 3回だけ2の目が出るとき。 (2) 1の目が2回以下出るとき。 解答(1) (2) ここで,正の数 p に対して p 0 =1 と決めてます(詳しくは,指数関数で紹介します)。上の例題1の(2)より5回中2の目が2回以下出る確率は 096




清 史弘 受験生諸君 さいころをn個投げて 出た目の積が10の倍数になる確率 は 出た目の積が2の倍数になる確率 と 出た目の積が5の倍数になる確率 をかけたものである 何て思っていないよね



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト
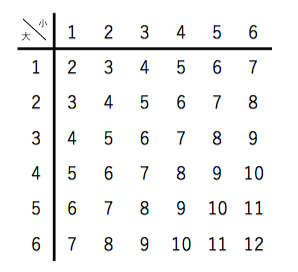
X3 確率論の基礎,確率空間の例 演習問題1 解答 ˇ 問題の難易度の目安基礎9 標準8 発展8 1(9)(算術的確率1) サイコロを無作為に2回振るとき,事象A:1回目の出た目が5である確率を,標本 空間を設定して求めよ. 解 (x 1;x 2)で1回目の出た目x問題3 正6面体のサイコロで1の目が出る確率を求めなさい。 → 解答 場合の数と確率の練習問題 問題1 次の問いに答えなさい。 → 解答 (1) 大きさのちがうサイコロA、Bを同時に投げたとき、サイコロの目の和が7になるのは何通りありますか。 (2) 区別のつかないサイコロを2つ同時に投げ(3) 無限回のサイコロ投げ 有限回だけサイコロを振る場合や根元事象の数が有限個のとき, (1), (2) で見たようにラプラス流の確率 で間に合う(根元事象の確率がすべて等しい場合も考えるというふうに一般化していますが) 何回も独立に サイコロ投げを続けることを考える その試行の結果として



確率の基本 サイコロを投げる 苦手な数学を簡単に




高校数学 数a 19 確率 さいころ編part 1 Youtube
さいころの目の最大値が3以下、3になる確率 4個のさいころを同時に投げるとき,次の確率を求めよ。 すべての目の出方は、 通りとなります。 あとで分数に形にして約分できることを考えて、 は計算せず、このままの形にしておきます。 どの目も (3通り)のどれかということになります。(a) 連続確率変数:結果の数値が隙間なく現れ得るとき. 身長,体重,ガソリンの消費量,到着時刻等々 (b) 離散確率変数 結果の数値がとびとびで並べられるとき またはいくつかの結果が出てくるが,それをとびとびの数字に 表せるとき. サイコロの目,1分間にある地点を通る自動車の数,世論調査問題 {9{サイコロを2 回投げて1 回目に出る目の数と2 回目に出る目の 数の和をx とするとき, x 2とx2 の確率分布の表を求めよ 問題 コインを3 回投げる 表の出る回数をx とし,表と裏の出る回数 の差の絶対値をy とする このとき,確率変数x;y の和(x y) と積xy の確率分布の表を求めよ



3つのサイコロ




サイコロの目の積 数学a 確率 Youtube
1 理論的な確率分布表に近づいていくはずです。なお,サイコロの{1, 2, 3, 4, 5, 6}の目のように,数字が区切れて並ぶような 3つのサイコロの確率の問題について 同時に投げたとき ・出る目の最小値が3以上の確率は (4/6)^3 ですが 1ー(2/6)^3 (全事象から2以下を引いている) とならないのはなぜでしょうか? ベストアンサー 数学・算数;サイコロを1回投げるとき サイコロ投げ有限母集団説を採用する •母集団から1個 ランダムに取り出 し数字を確認す る作業を、x (確 率変数)とする。 1 2 3 4 5 6 母集団 割合はそれぞれ「6 分の1」である。 確率




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校の数学についてです 3つのサイコロを同時に投げた時 すべて異な 数学 教えて Goo
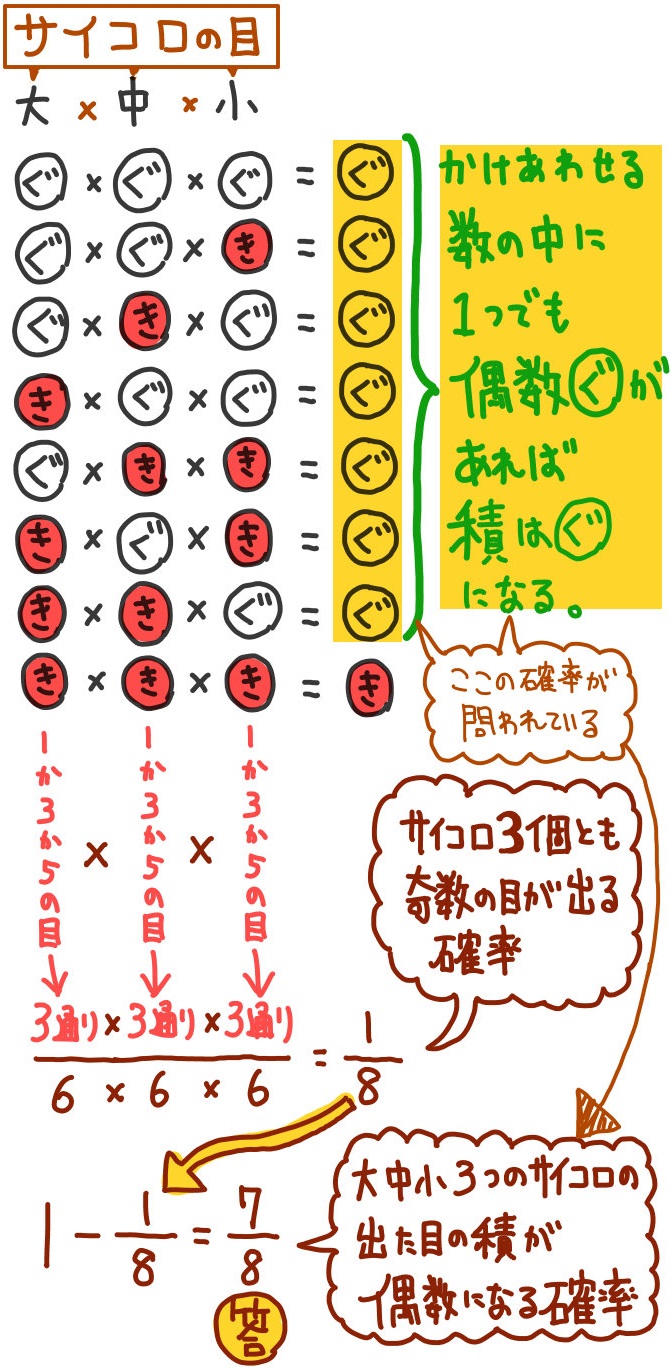
もっと見る その他の回答 (1) 26 回答No1;よって,求める確率は 3 3 3 6 4 -3 = 216 37 7 袋a には赤玉3 個と白玉5 個,袋b には赤玉4 個と白玉2 個が入っている。袋a から1 個,袋b から 1 個の玉を取り出すとき,2 個が異なる色の玉である確率を求めよ。 解答 袋a から玉を取り出す試行と,袋b から玉を取り出す試行は独立である。 2 個が例えば、サイコロを3回振るとき、 「1回目奇数」「2回目偶数」「3回目奇数」 となる確率は、 \( p=\displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}\) と求めることができるということです。



1



5 3 確率サイコロ 日立市民科学文化財団
まず、例えば、サイコロ3個を同時に振って、「1」の目が1つでも出る確率は、 1個目:1/6 2個目:1/6 3個目1/6 = 3/6 = 1/2 の考え方になると思います。3 まとめ:確率 の大原則・大数の法則 31 共有 32 いいね 確率1/6とは、6回のうち1回起こるということではない 高校で学習する確率では、答えが分数になります。 絶対に起こらない事象の場合は確率が 0 、絶対に起こる事象の場合は確率が 1 で、サイコロの振り方で バラツキは違うか •サイコロを何回も振ったときの, サイコロの出目 の分布を考えてみよう •サイコロの出目は, 平均35を中心にばらつく •サイコロ投げのように確率的試行を繰り返したと きにも分布ができる そのときの分布を確率




サイコロの確率分布のモデリング




数学a 大中小の3個のサイコロを投げる時 出る目が全て異なるときの確 高校 教えて Goo
サイコロの目の出る確率 確率が気になって調べたら意外と高かったので安心してダイスを振れました。 3d6で特定の出目が1回以上出る確率が43%(正確には%)なら出せる。 遊びをまじめに。 試行回数を重ねれば数字は収束する。 100面体のサイコロで試行回数を重ね収束しないまま例えばパチンコ屋に行き1/100の確率のパチンコ台を打てばそこで確率が収束し確率と確率変数 サイコロを投げ, 3か6の目が出たら出欠を取る 1,2,4,5の目が出たら出欠は取らない サイコロの目の全ての出方は Ω={1,2,3,4,5,6}←標本空間( sample space ) ©ATSUTO NISHIO 出欠を取るという事象 :E 1={3,6} 出欠を取らないという事象:E




高校数学a 反復試行の確率 基本 Ncrp R 1 P N R 受験の月




サイコロの確率 Youtube




中学数学 さいころ2個の確率問題をパターン別に解説 数スタ




高校数学a 余事象の確率 少なくとも かつ 少なくとも の確率 受験の月




大小 シックボー のルールと遊び方 カジノ初心者向け カジペディア



3つのサイコロ
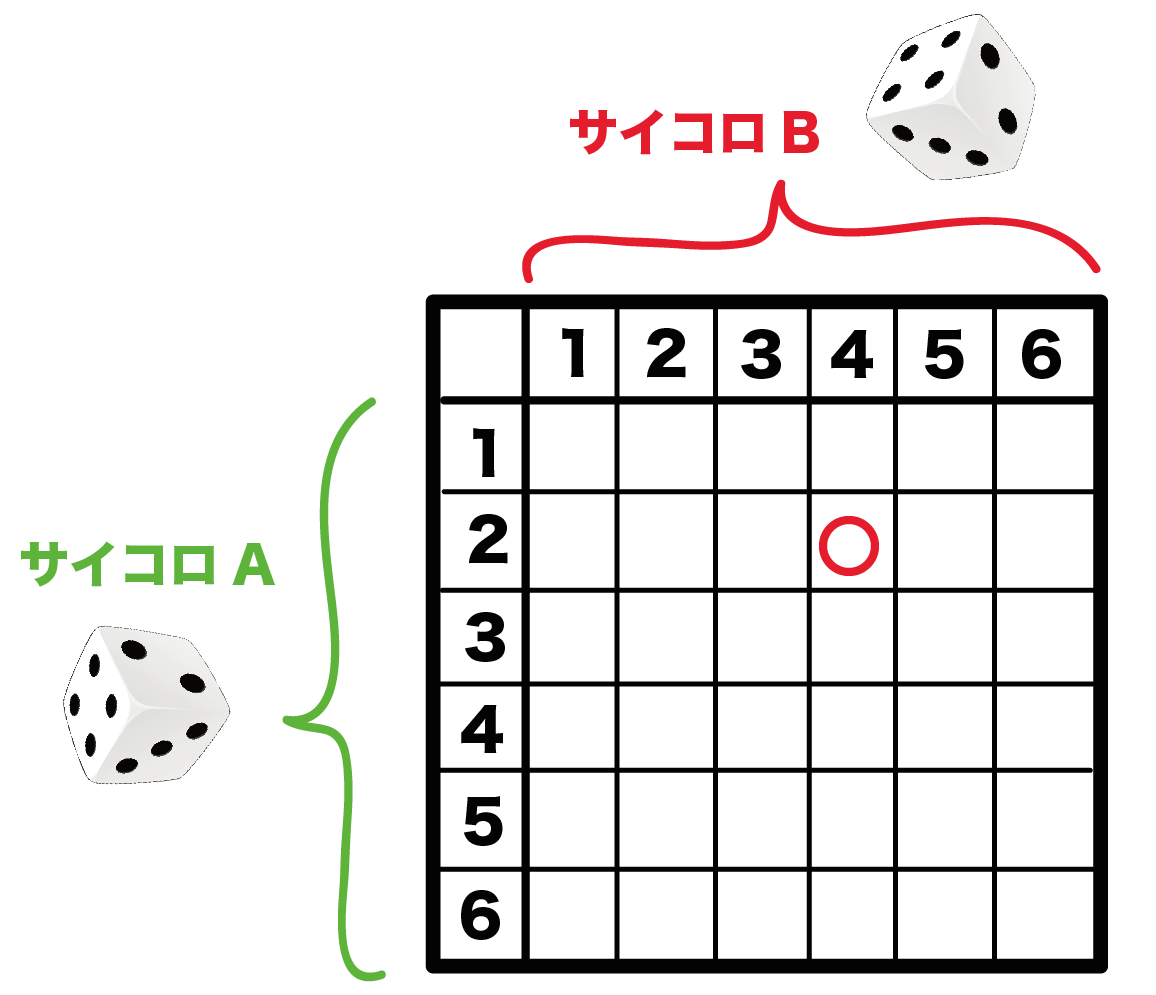



簡単計算 2つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校入試 さいころ 3個 の確率 Youtube



3つのサイコロのうち2つが同じ目になる確率を教えてくださいよろしくお Yahoo 知恵袋




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数ia確率 サイコロ3つで3ケタの数字を作る 北海道大18文系第3問 Mm参考書




1個のさいころを5回投げて目の和が10以下になる確率 怜悧玲瓏 高校数学を天空から俯瞰する




さいころを2個同時に振ったとき 8なる確立 立方体のさいころを2個同 数学 教えて Goo



大中小3個のサイコロを同時に投げる すべて3以下の数の目が出る場合は全 Yahoo 知恵袋



サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ




無料ダウンロードサイコロ 問題 解き方 子供のための最高のぬりえ




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学



さいころ3個同時に投げたとき 3個とも同じ目が出る確率を求めなさい Yahoo 知恵袋




条件付き確率とは 公式を使ってサイコロ 玉の問題を解いてみよう くじ引きを用いた例題付き 高校生向け受験応援メディア 受験のミカタ




中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun




中学数学の確率 コインとサイコロの問題の解き方と樹形図 リョースケ大学




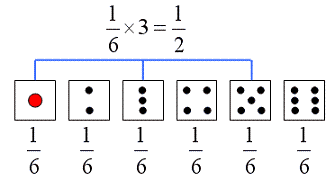
サイコロでゾロ目がでる確率を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



2個のサイコロを同時に投げるとき 異なる目が出る確率



3つのサイコロを同時に投げたとき 3つとも同じ目が出る確率 2つが同じ目で1 Yahoo 知恵袋




後編 サイコロ3つのうち1 2個の出目を当てる 大小 シックボー の確率と配当まとめ カジラグ



中学数学 確率 さいころ 中学数学の無料オンライン学習サイトchu Su




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学




2つのサイコロを振ったとき 出易い合計数はあるか わけいブログ



数学で 3個のサイコロを同時に投げるとき 次の確率を求めよ Yahoo 知恵袋



一色パの難しさ パズドラ エクレア牧場
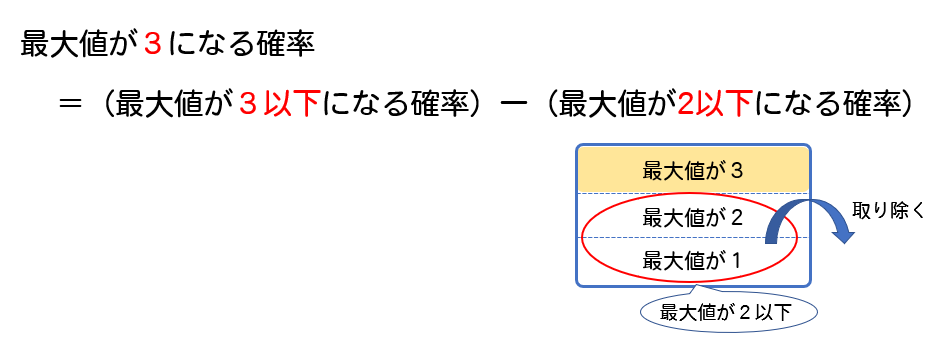



数学a サイコロの最大値が5 最小値が2になる確率はどうやって考える 数スタ




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学




サイコロの出た目の最小公倍数の確率の問題です F1 数学 箱根駅伝ブログ
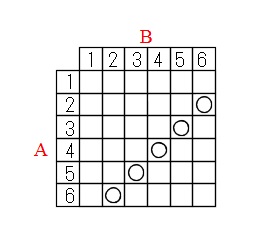



サイコロを2つまたは3つ以上振る確率の求め方と重複試行
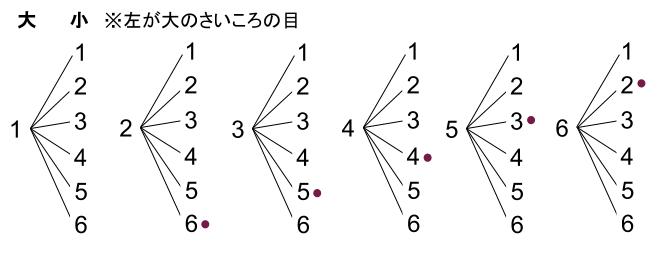



中学数学 確率 さいころ 中学数学の無料オンライン学習サイトchu Su




3個のさいころを同時に投げるときの確率の問題です Clearnote



3つのサイコロを振って1 2 3が出る確率と1 1 1が出る確率って同じ Yahoo 知恵袋
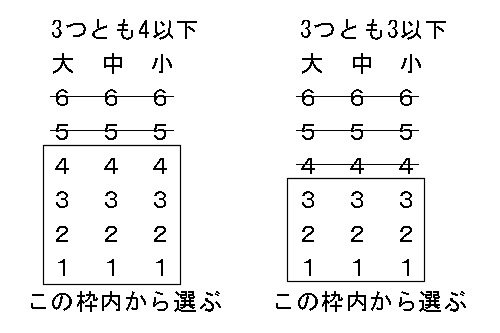



サイコロを2つまたは3つ以上振る確率の求め方と重複試行




3個のさいころを同時に投げるとき 次の場合の確率を求めよ Clearnote




サイコロ 問題 解き方 ニスヌーピー 壁紙




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学



大中小の3個のサイコロを投げるとき 次の確率を求めよ 1 Yahoo 知恵袋



1
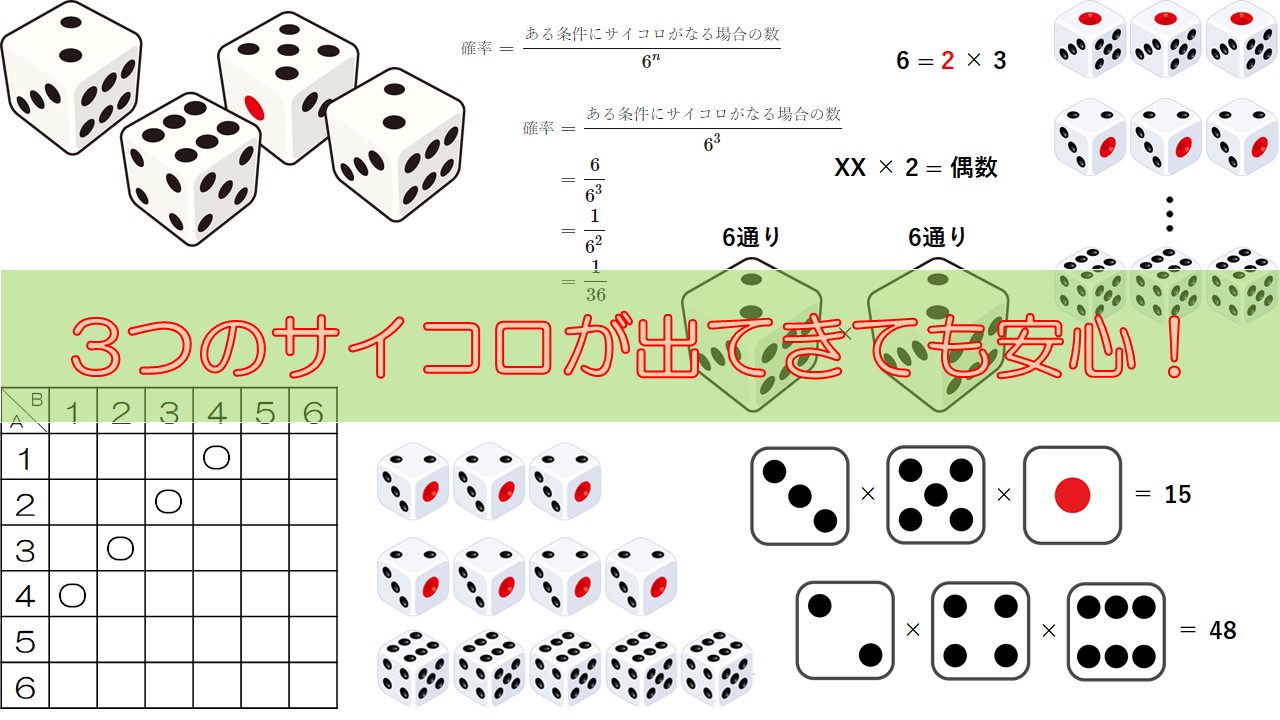



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト



さいころ 球 カードの確率の問題 Of 京極一樹の数学塾会員頁



サイコロの確率の問題 京極一樹の数学塾




確率の計算 サイコロを投げる場合 数学の偏差値を上げて合格を目指す




大 中 小3個のさいころを同時に投げるとき 1 3個とも同じ目が出る確率 Clearnote




2つのサイコロの目の合計が偶数になる確率の出し方 優しく教えて下さ 中学校 教えて Goo




サイコロの和と多次元立方体の関係 小人さんの妄想



数学i Aチェック リピート 第8章 1確率とその基本性質 4 さいころの確率 Pukiwiki




大中小の三個のサイコロを投げる時の確率 は出る目がすべて異なる Clearnote




中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




この問題は サイコロ3つを区別してますか セットアップ Clearnote




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



確率は賭け事の理論



1




反復試行の確率 3つの事象があるときのやり方は 数スタ



13 Introduction To Experimental Mathematics Ii By D Furihata




中2数学 2つのサイコロを投げるときに樹形図描く奴wwwwwwwwww 確率 牛乳屋黄三郎の雑感ブログ




高校数学 数a 勉強動画 確率 さいころ編 Part 3の問題 19ch



1




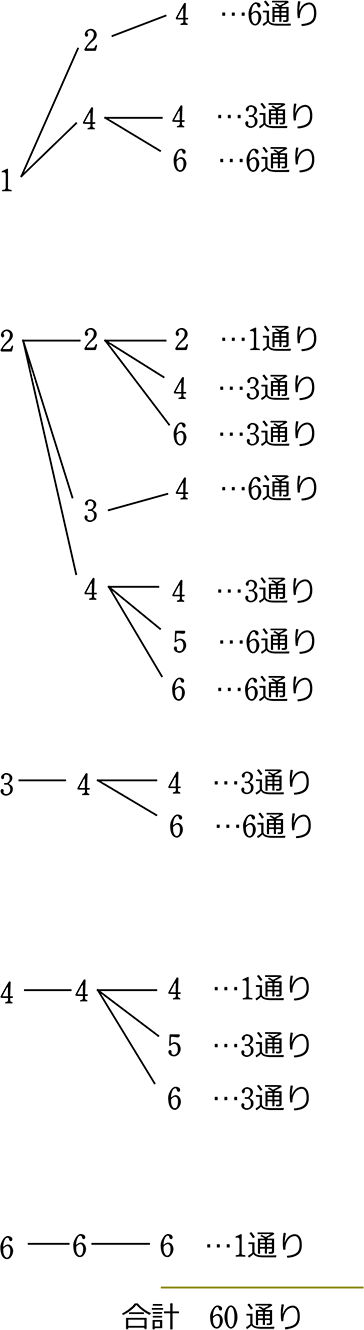
中学受験算数 サイコロ3つでも楽勝 和が6の倍数になる通り数を数えろ 毎日1題中学受験算数24 Youtube
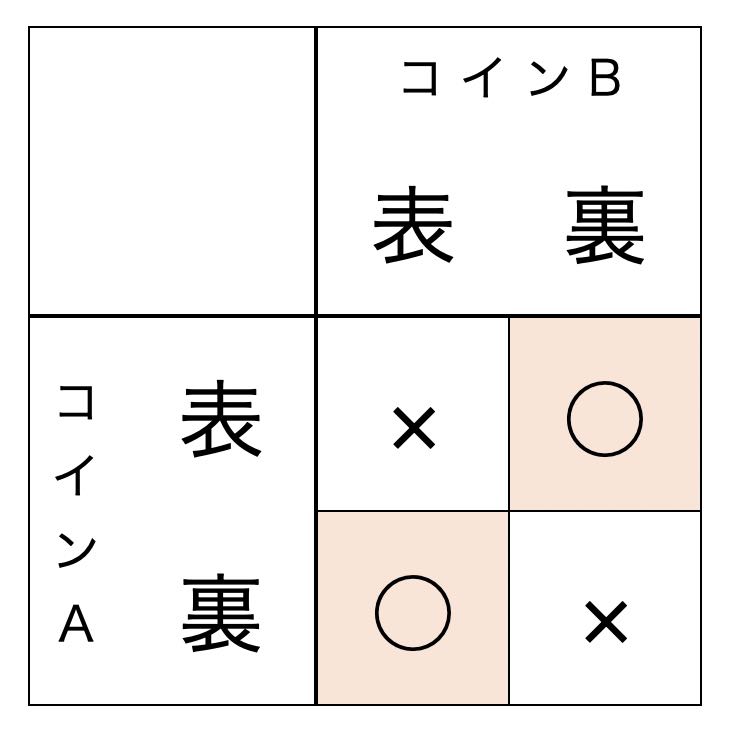



確率の計算ができないキミへ 数学a スタディクラブ情報局



確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾



反復試行の確率の式の意味 大学受験の王道




株 日科技研 第24話 インドサイコロの確率計算 六一学者の千字一話 会員広場



数学を極める 1 確率を極める 予備校なら武田塾 河内松原校




なぜこのときさいころ3個を区別しないで考えるのでしょうか Clearnote



5 3 確率サイコロ 日立市民科学文化財団




サイコロの出た目を使った三角形を作る確率の問題です 大学入試数学問題の解説 解答



インターネットカジノ オンラインカジノ Com



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




2つのサイコロの確率 Youtube




ヾ しw玉 ノ このチンチロやってみた 一投目でいきなりゾロ目が出たぞ サイコロを3つ振ってゾロ目になる確率 は 36分の1だそうです 1個めはどれでもよくて 2個めと3個めが同じになる確率を出すからだと うーん 運を使い果たしてしまったかな し
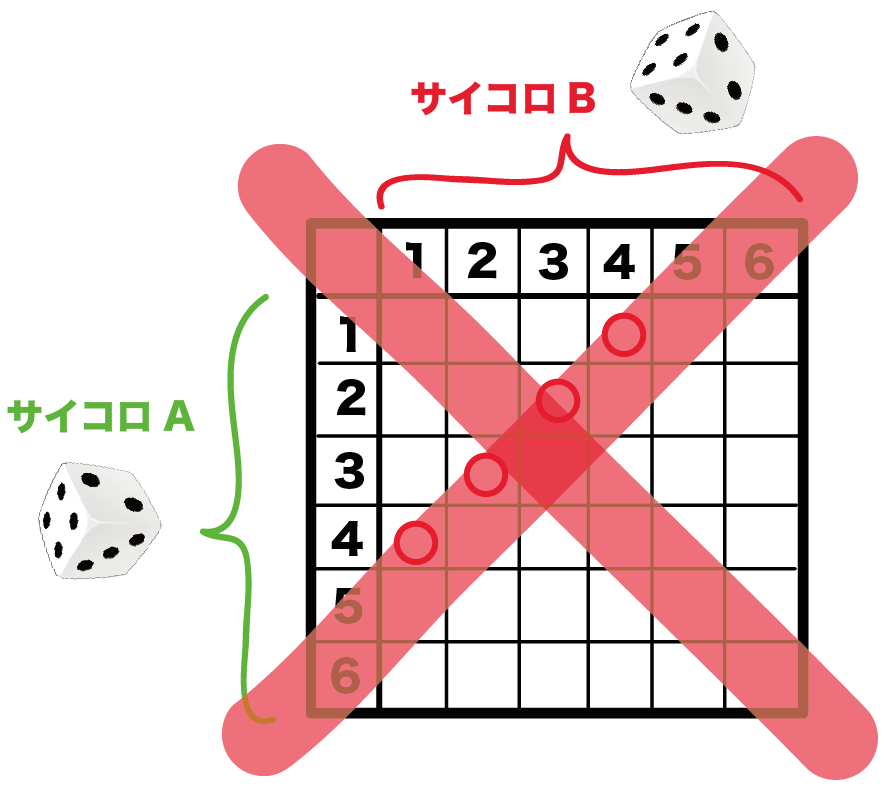



中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




素朴な疑問なのですが 5 6 6と6 6 6とあるのですが 150以上になる Clearnote
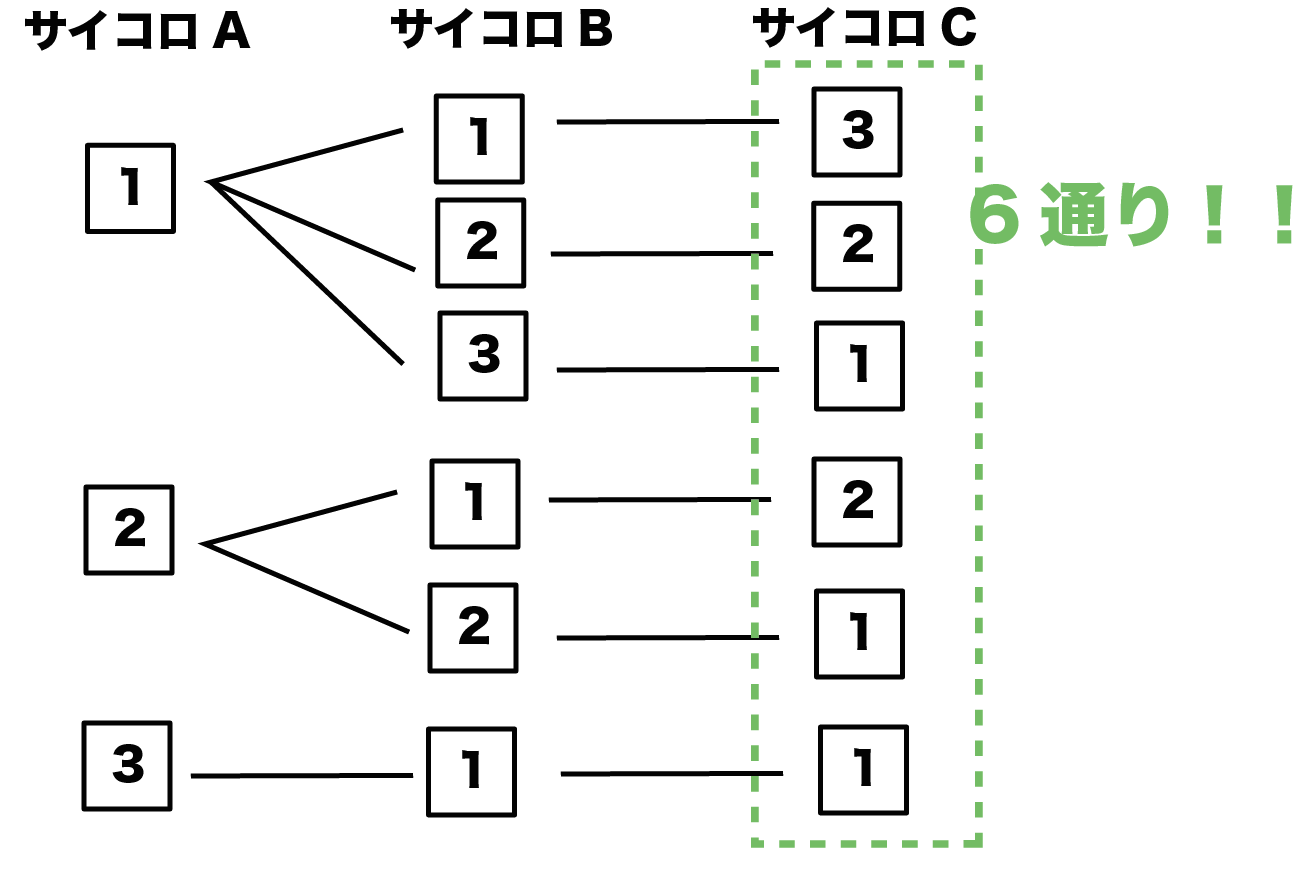



中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




高校数学 数a 20 確率 さいころ編part 2 Youtube




サイコロ10コの出目の合計を当てろ やぐち建築士の備忘録
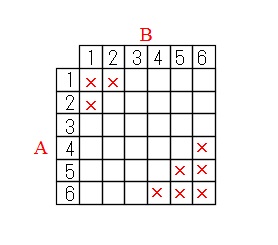



サイコロを2つまたは3つ以上振る確率の求め方と重複試行



インターネットカジノ オンラインカジノ Com




場合の数 大中小3つのサイコロを投げるとき何通り 奇数 偶数 4の倍数 数スタ




03 号 32面体サイコロ Astamuse




サイコロ3個を振った時の確立について質問です サイコロ3個を振っ 数学 教えて Goo




反復試行




前編 出目の組み合わせから考える 大小 シックボー 賭け方別の確率と配当まとめ カジラグ
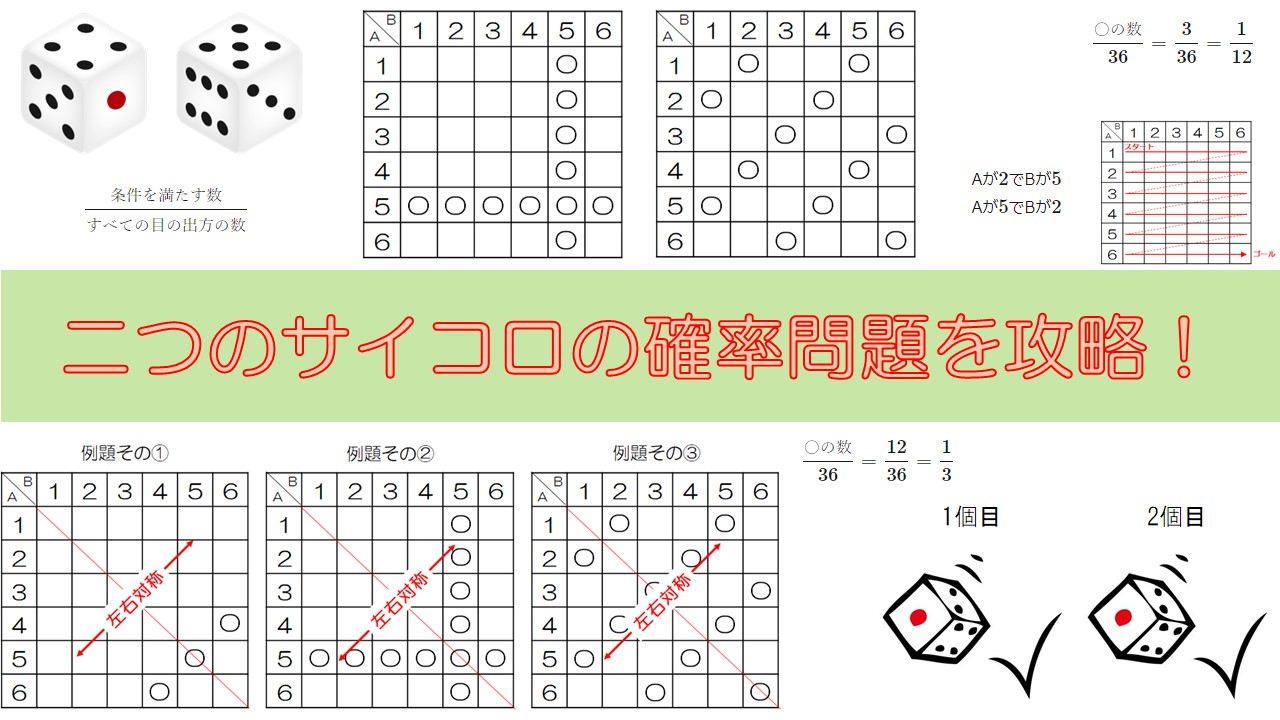



中学2年数学 確率 二つのサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト



3個のさいころを同時に投げるとき目の和が7の倍数になる確率を求めよ という問 Yahoo 知恵袋



0 件のコメント:
コメントを投稿